Contrast Sensitivity Paradigm
2D Spatial Vision Modeling
Applications

List of Slides:

Stimulus Spatial Frequency
Stimulus Contrast
Gabor Stimuli
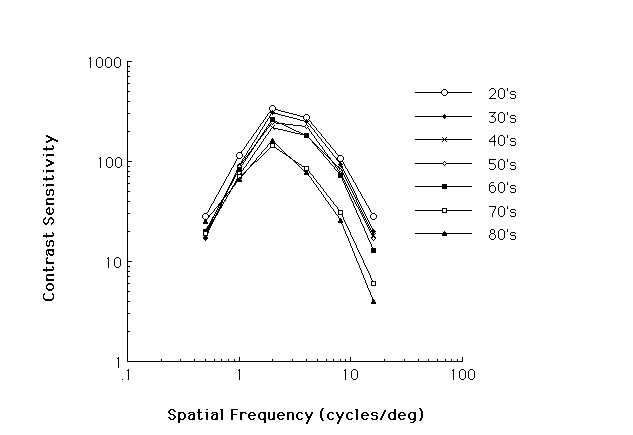
The Contrast Sensitivity Function
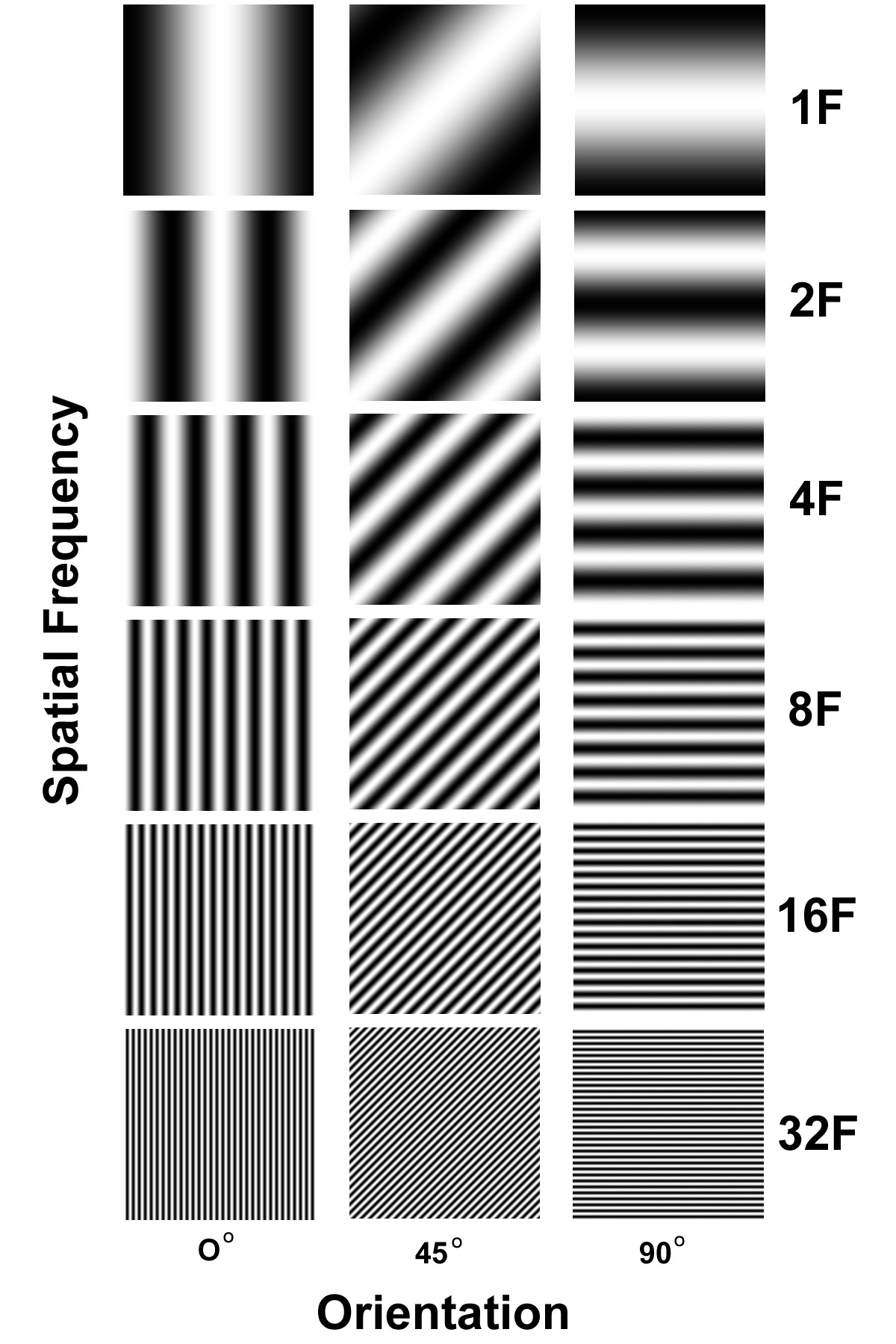
SF x Orientation Stimulus Space
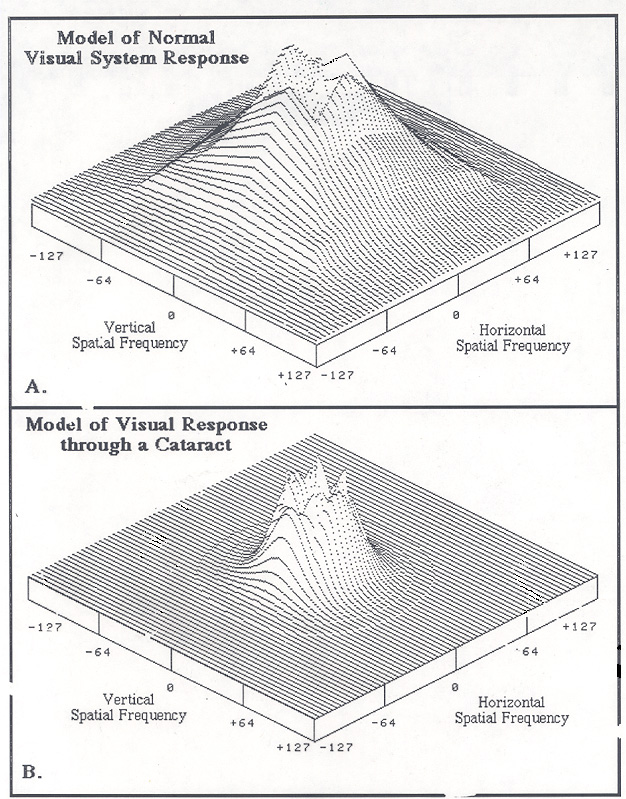
2D-CSF Models
Filtering Stimuli through 2D-CSF Models


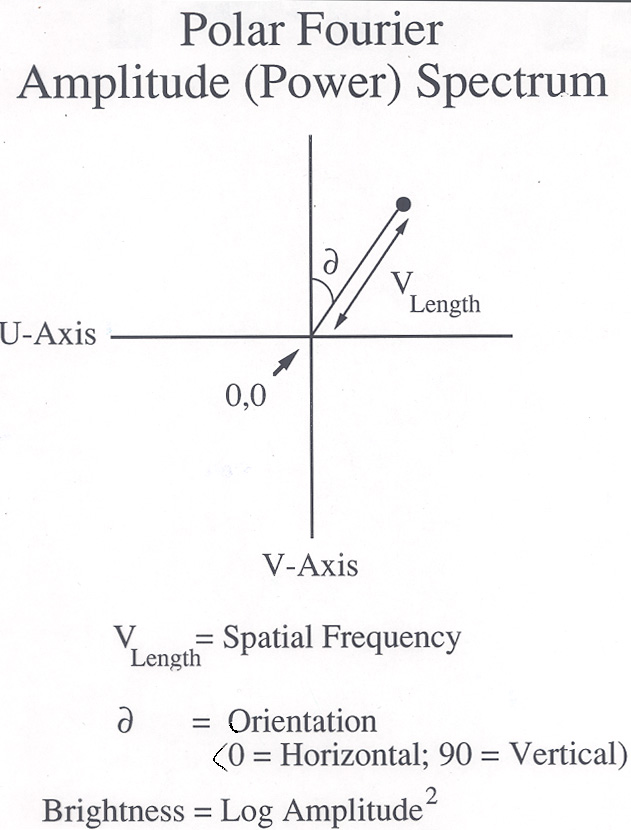
2D-Fourier Axes
2D-Fourier Data Point
2D-Fourier Bands
Simple Stimulus 2D Fourier Spectra
2D-CSF Models
Filtering Stimuli through 2D-CSF Models

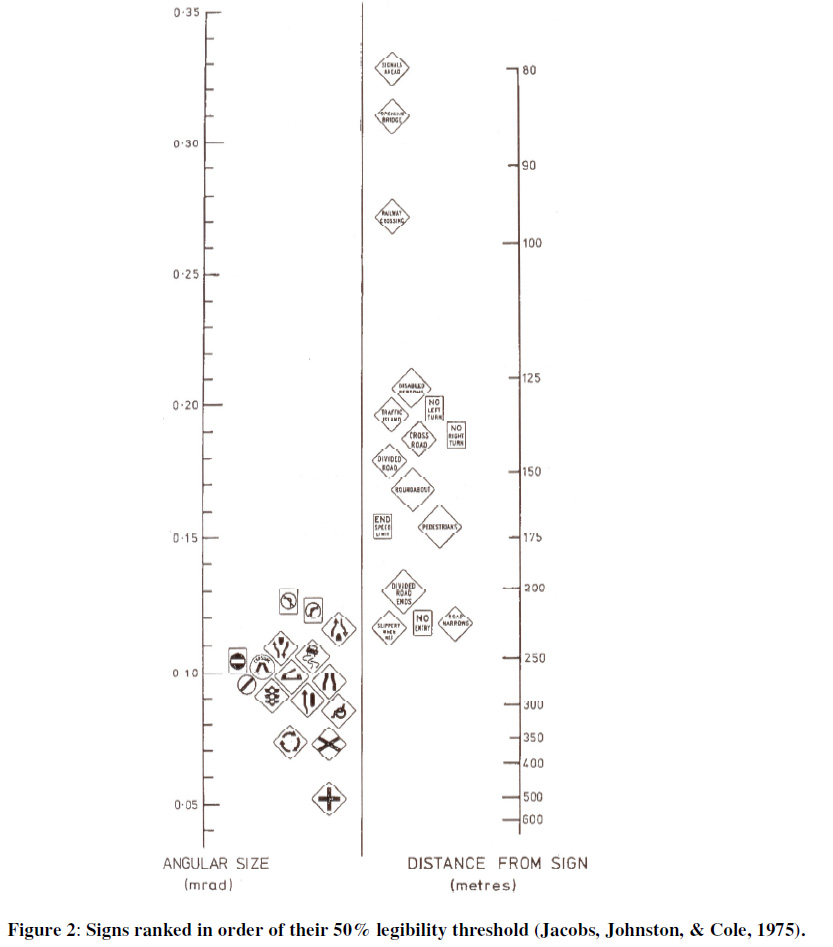
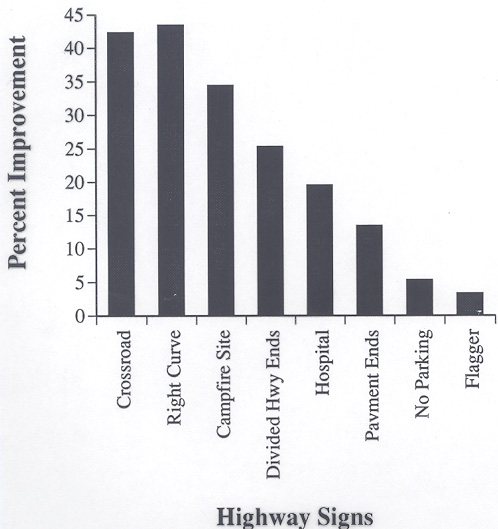
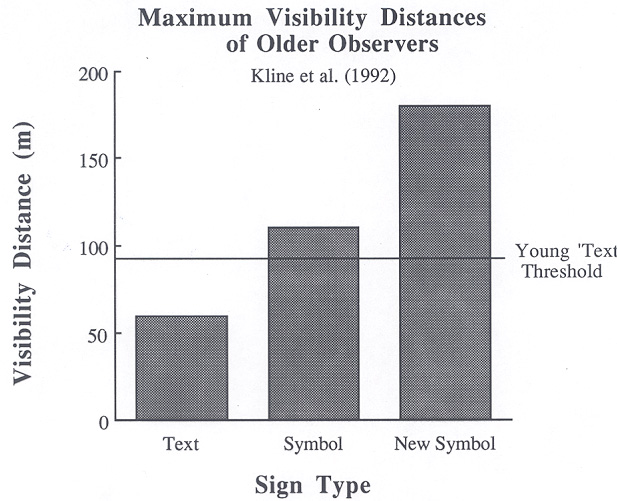
Symbol Signs
2-Way Traffic
Filtered Signs
Recursive Blur Sample Stimuli
Recursive Blur Results
Falling Elephants

The Fourier Theorem and Visual Form Perception

Provides the basis for a universal mathematical language for the description of images and imaging systems

Sine wave functions can be used to describe ANY visual image

Sine wave functions can be used to describe the efficiency/sensitivity of the human system

Given this COMMON METRIC for describing both the stimulus (image) and the visual system (observer), the Fourier theorem can be applied to determine the "goodness of fit" between any stimulus form and any observer (normal; infant; cataract; etc.)

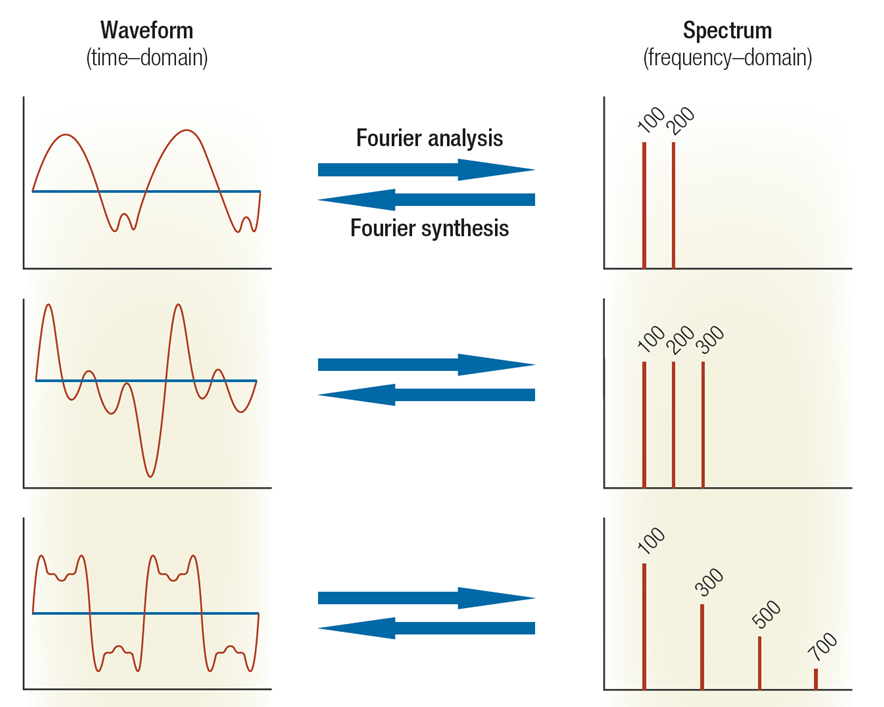
The Fourier Theorem states that:

Any complex, 1-dimensional function can be expressed as an additive series of sinusoidal functions varying in (1) frequency, (2) amplitude and (3) phase.

Fourier Analysis of 1-D Sound Stimulus

Fourier Synthesis of 1-D Sound Stimulus

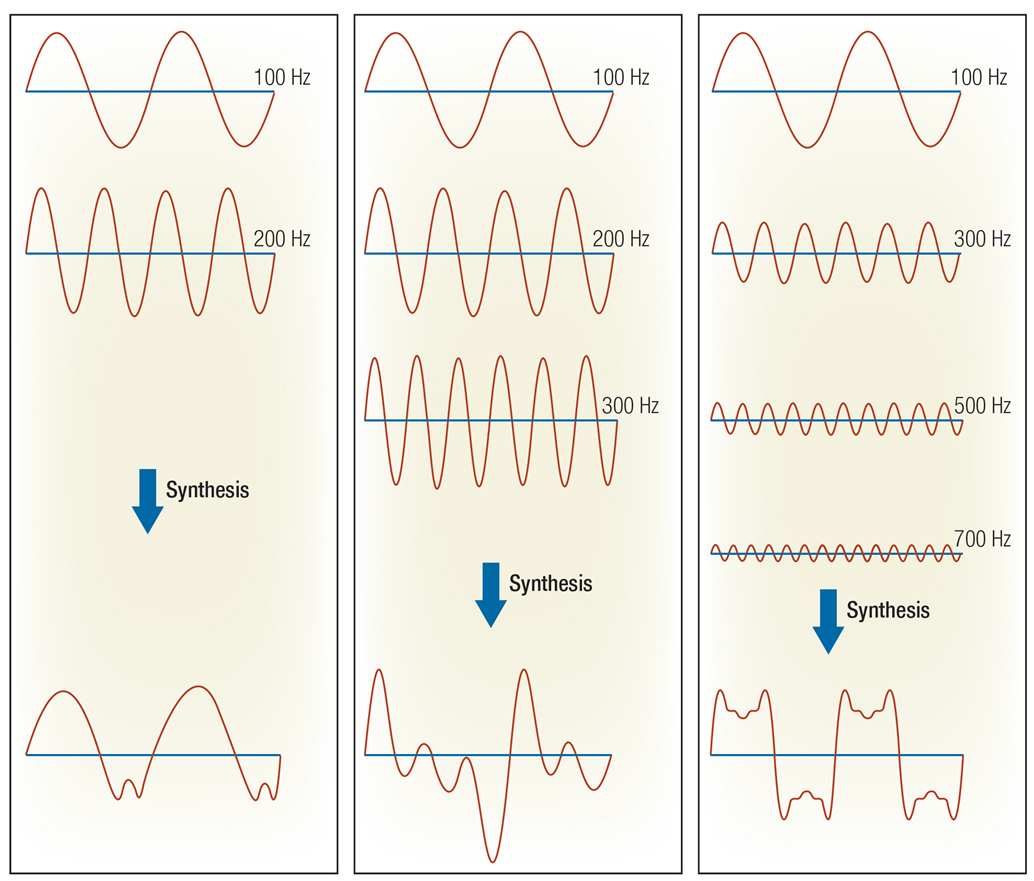
The Fourier Theorem can be generalized to 2-Dimensional stimuli (e.g., images) with the addition of a 4th sine wave parameter:

(1) frequency
(2) amplitude
(3) phase
(4) orientation

Hence, 2-Dimensional Sine Wave Luminance Gratings become the basis for describing visual stimuli as well as probing the visual system's sensitivity to these same images.

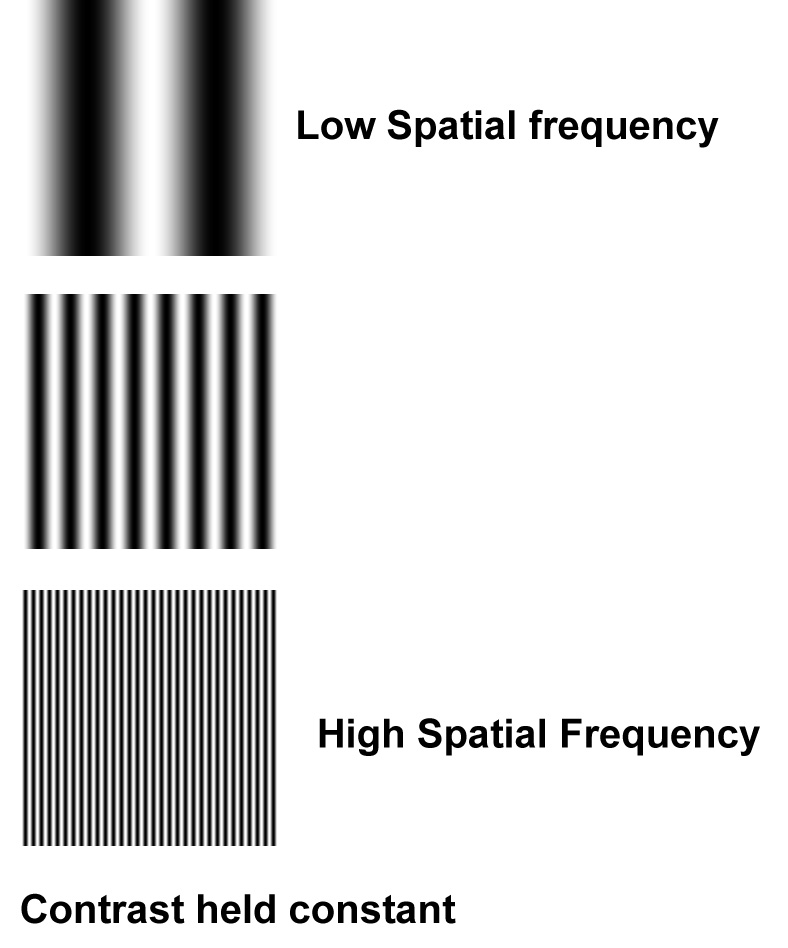
Gabor Gratings of Increasing Spatial Frequency

Simple Contrast Sensitivity Function